Denne artikel er dedikeret til at guide dig gennem processen med at beregne den kraft, en aktuator kræver for at løfte lasten i din applikation. Der er et par faktorer involveret for at finde den rigtige kraft, herunder lasten, den vinkel, hvormed den skubbes, og lastens størrelse.
Lige op versus vinklet montering
Retningen af lineær aktuator Kraften bestemmer den beregning, der skal anvendes. Aktuatoren kan monteres lige op eller i en vinkel. Nedenfor diskuterer vi begge konfigurationer og hvordan man beregner kraften fra den lineære aktuator i hvert scenarie.
Monteret lige op
For at beregne en aktuators træk-trykkraft, hvis den er monteret lige op, skal den nødvendige aktuator have den samme kraftklassificering som den nødvendige vægt. Man bør dog altid vælge en aktuator med en højere kraft end lasten for at være på den sikre side. Dette skyldes friktion og andre faktorer, der kan øge den nødvendige kraft til at bevæge lasten. Som på billedet nedenfor, for eksempel, hvis lasten er 50 lb, skal aktuatorens kraftklassificering (F) være større end 50 lb.
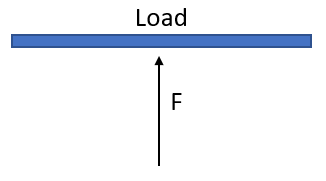
Monteret i en vinkel
Når lasten og aktuatoren skal monteres i en vinkel, ændres metoden til at beregne aktuatorkraften betydeligt. Da aktuatoren skubber i en vinkel, vil den i de fleste tilfælde kræve en højere kraft end den faktiske last for at løfte den.
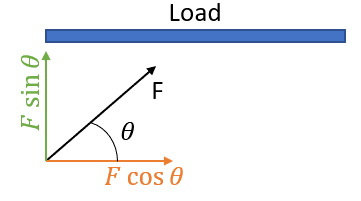
Ovenstående figur viser perfekt de faktorer, man skal overveje, når man beregner kraften for en vinklet montering. Hvis lasten f.eks. er 50 lb, og den er monteret i en vinkel på 45° (θ) i forhold til jorden, skal man sikre, at kraften vinkelret på lasten, F sinθ, i dette tilfælde er større end eller lig med 50 lb.

Det betyder, at hvis du skubber en last på 23 kg i en vinkel på 45°, skal du bruge en lineær aktuatorkraft, der kan håndtere en belastning på mindst 34 kg.
Alternativt, hvis du planlægger at skubbe lasten sidelæns og gerne vil skubbe den i en vinkel på 60°, er det den samme ligning, men ændret for at tage højde for den retning, du skubber din applikations last i. Dette er vist på billedet nedenfor.
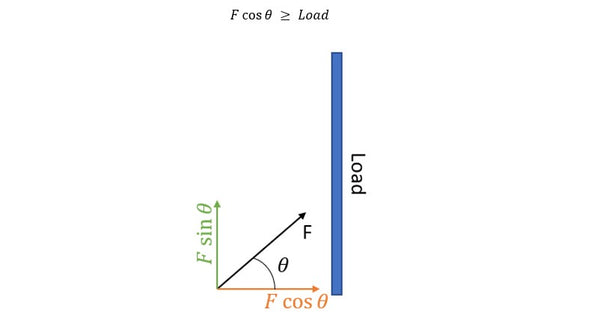
Du vil også bruge den samme metode som vist tidligere, som vist i nedenstående ligning.

Sidste ord
Kort sagt repræsenterer ligningerne nævnt i denne artikel hvert scenarie, hvor din montering af lineær aktuator er vinkelret på belastningen. Brug disse beregninger til at bestemme den nødvendige kraftklassificering for din aktuator, så du sikrer, at du aldrig underskrider den mængde, du har brug for. Det er et simpelt trin, men det kan spare dig en masse tid, når du vælger den rigtige lineære aktuatorkraft. Progressive Automations tilbyder flere vejledninger og ressourcer til at vælge den rigtige lineære aktuator til din applikation. Når du har valgt den rigtige kraft, kan du bestemme slaglængde, spænding og hvilke kontrolmetoder du vil bruge. Hvis du har brug for yderligere hjælp til, hvordan du vælger en lineær aktuator til din applikation, kan du ringe til os på 1-800-676-6123 eller sende os en e-mail på sales@progressiveautomations.com.




